| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- 최소공배수
- 스프링뼈대
- 유클리드호제법
- replaceAll()
- 최대공약수와 최소공배수
- 스프링
- 동일성과 동등성
- 자바 스트링
- 자바 최소공배수
- islowercase()
- sql 데이터형 변환
- 스프링환경설정
- 래퍼타입
- 자바 유클리드
- 최대공약수
- while과 two-pointer
- 자바 최대공약수
- toLowerCase()
- Git사용법
- stringbuilder의 reverse()
- isuppercase()
- ineer join
- git 컨벤션
- 베주계수
- 모던자바
- StringBuilder
- addDoc
- string
- string과 stringbuilder
- 프로그래머스 레벨1
- Today
- Total
주노 님의 블로그
프로그래머스 - 최대공약수 와 최소공배수 (유클리드 호제법) 본문
https://school.programmers.co.kr/learn/courses/30/lessons/12940
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
두 수를 입력받아 두 수의 최대공약수와 최소공배수를 반환하는 함수, solution을 완성해 보세요. 배열의 맨 앞에 최대공약수, 그다음 최소공배수를 넣어 반환하면 됩니다. 예를 들어 두 수 3, 12의 최대공약수는 3, 최소공배수는 12이므로 solution(3, 12)는 [3, 12]를 반환해야 합니다.
제한 사항- 두 수는 1이상 1000000이하의 자연수입니다.
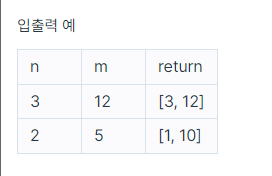
입출력 예 #1
위의 설명과 같습니다.
입출력 예 #2
자연수 2와 5의 최대공약수는 1, 최소공배수는 10이므로 [1, 10]을 리턴해야 합니다.
풀이
알고리즘 문제에 수학만 나오면 시간을 엄청 잡아먹는 나
놀랍게도 한시간 정도 쓴듯 이문제에만..
약수 : 어떤 정수에 나누어 떨어지는 수
최대공약수 : 두개 이상의 정수의 공통된 약수 중에서 가장 큰 값
최소공배수 : 두개 이상의 정수의 공통된 배수 중에서 가장 큰 값
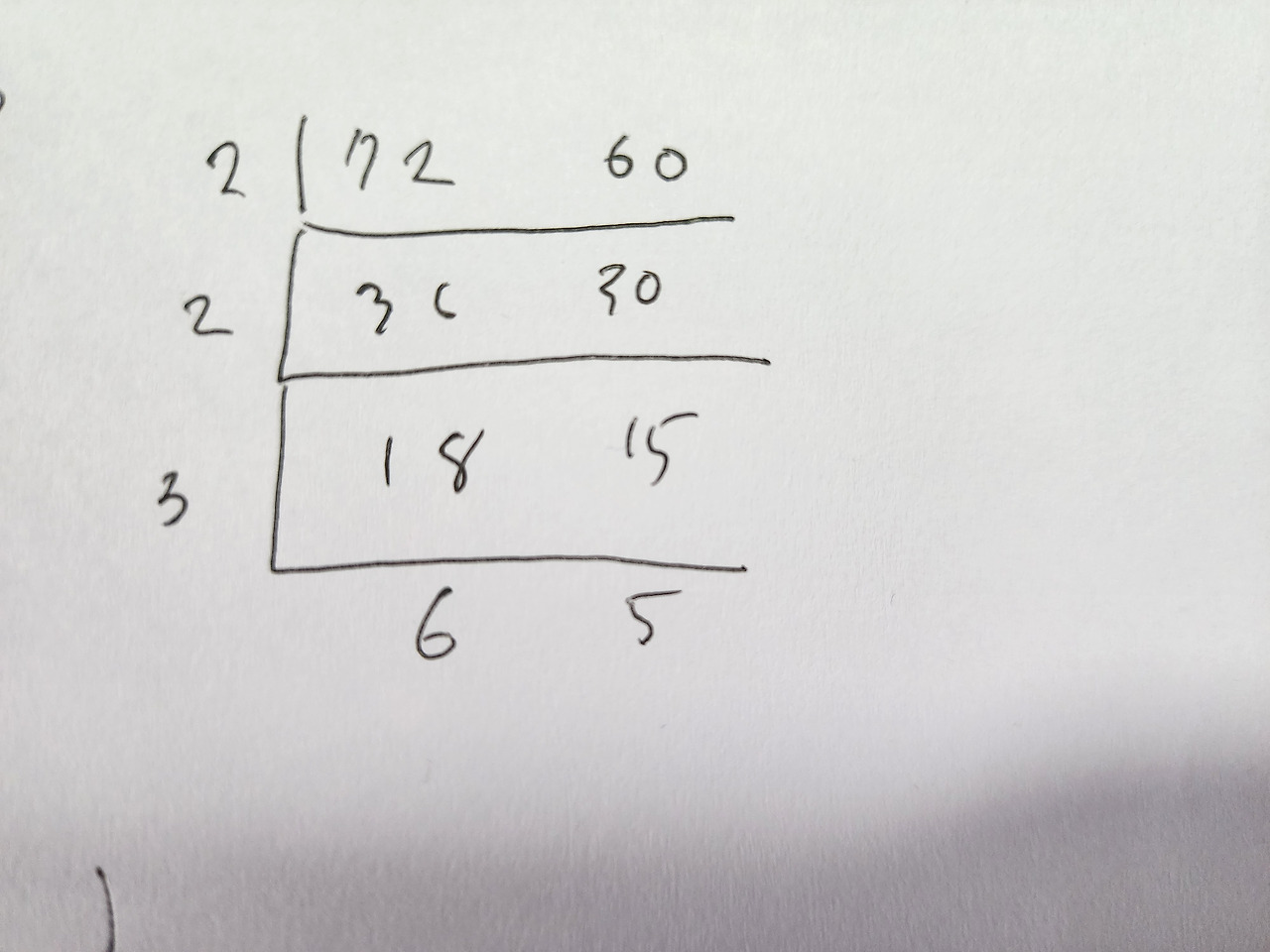
72와 60의 최대공약수 : 2*2*3 =12
72와 60의 최소공배수 : 2*2*3*6*5 = 360이다
최대공약수와 최소공배수를 자바로 어떻게 구현할 수 있을까?
import java.util.ArrayList;
import java.util.List;
public class GCDByPrimeFactors {
public static void main(String[] args) {
int a = 72;
int b = 60;
System.out.println(a + "와 " + b + "의 최대공약수: " + gcdByPrimeFactors(a, b));
}
public static List<Integer> primeFactors(int n) {
List<Integer> factors = new ArrayList<>();
int divisor = 2;
while (divisor <= n) {
if (n % divisor == 0) {
factors.add(divisor);
n /= divisor;
} else {
divisor++;
}
}
return factors;
}
public static int gcdByPrimeFactors(int a, int b) {
List<Integer> factorsA = primeFactors(a);
List<Integer> factorsB = primeFactors(b);
List<Integer> commonFactors = new ArrayList<>();
for (int factor : factorsA) {
if (factorsB.contains(factor)) {
commonFactors.add(factor);
factorsB.remove(Integer.valueOf(factor));
}
}
int gcd = 1;
for (int factor : commonFactors) {
gcd *= factor;
}
return gcd;
}
}
이렇게 무지막지하게 길어지게 된다.
수학자들은 최대공약수를 구하는데 아주 간편한 계산식을 발견했다
유클리드 호제법이라는 공식이다

예 글씨 못씁니다.
선형대수학에서 베주계수를 찾으려고 유클리드 호제법을 이용한것이 떠올랐다.
유클리드 호제법은 두 수의 최대공약수를 찾는 방법이다
주어진 두 수 a와 b에 대하여 a를 b로 나눈 나머지를 구하고.
이 나머지를 b라고 하고 원래의 b값은 새로운 a가 되며
나머지가 0이 될때까지 반복을 한다.
a=b*몫+나머지1
b=나머지1*몫+나머지2
나머지1=나머지2*몫+나머지3
이런식으로 계산하여 마지막 나머지가 없을때 마지막으로 나온 나머지값(a)이 최대공약수 이다.
즉
a=b*몫+나머지1
b=나머지1*몫+나머지2
나머지1=나머지2*몫+나머지3
이런식으로 진행된다면 b의값은 두번 사용한다 b의값을 임시 저장할 temp 변수에 넣어두고
b=a%b(나머지 1의값)
a=temp (다음번에 돌아갈 b)
이렇게 되는것이다 우리는 나머지값만 파악하면 된다.
따라서 나머지가 0이될때까지 반복문을 돌면된다
public static int gcd(int a, int b) {
while (b != 0) {
int temp = b; // 현재 b 값을 임시 저장
b = a % b; // a를 b로 나눈 나머지를 b에 저장
a = temp; // 이전 b 값을 a에 저장
}
// 반복이 끝나면 a에 최대공약수가 남는다
return a;
}이렇게 구현하면 최대공약수가 나오게된다.
최소공배수는 a*b/gcd(a,b)가 된다
구현 결과
class Solution {
public int[] solution(int n, int m) {
int[] answer = new int[2];
answer[0] = gcd(n,m);
answer[1]=lcm(n,m,answer[0]);
return answer;
}
public int gcd(int a, int b)
{
while (b!=0)
{
int temp = b;
b = a % b;
a = temp;
}
return a;
}
public int lcm(int a, int b, int gcd)
{
return (a*b)/gcd;
}
}
'공부 > 코딩테스트(java)' 카테고리의 다른 글
| String, StringBuilder을 사용한 간단한 코딩테스트 문제풀이 (0) | 2024.08.19 |
|---|---|
| 프로그래머스 - 두 개 뽑아서 더하기 (중복을 허용하지 않는 Set) (0) | 2024.08.09 |
| 프로그래머스 - 로또의 최고순위와 최저순위 (java) (0) | 2024.07.29 |



